問題コーナー（第3回）解答

f:id:yootaamath:20170221210253p:plain
この問題は難しかったかと思います。
15°って割と使うのが難しいんですよね。しかも27°という数字まであります。
解答です。

用意していた解答

この解答はやや複雑です。角の二等分線定理を使います。
まず、図のように点 ${A,B,C,D}$ とおきます。
f:id:yootaamath:20170221210253p:plain
そして、 ${DA}$ の延長に ${\angle ABE=15^\circ}$ となるように点 ${E}$ を、
${DC}$ の延長に ${\angle CBF=27^\circ}$ となるように点 ${F}$ をとります。
f:id:yootaamath:20170221210255p:plain
つぎに四角形 ${BFDG}$ が平行四辺形となるように、
つまり ${\triangle BDF\equiv \triangle DBG}$ となるように点 ${G}$ をとります。

すると図のようになります。（見覚えのある人もいるかもしれません）
f:id:yootaamath:20170221210257p:plain
ここで、直線 ${DG}$ に関して点 ${E}$ と同じ側に、 ${\triangle HDG}$ が正三角形となるように点 ${H}$ をとります。
f:id:yootaamath:20170221210259p:plain
すると、二辺挟角相等より ${\triangle GDE \equiv \triangle HDE}$ より ${EH=EG}$
よって ${\angle EHG=36^\circ}$ となります。
また、 ${\angle GHD=2 \angle GBD}$ 、 ${HG=HD}$ より点 ${H}$ は三角形 ${BDG}$ の外心となるので、 ${HB=HG}$ となります。よって ${\angle EBH=36^\circ}$ です。
そして簡単な角度計算で ${\angle BEH=\angle BHE =72^\circ }$ がわかり、 ${EB=HB}$ がわかります。
よって、 ${BE=DG}$ となります。
f:id:yootaamath:20170221210301p:plain
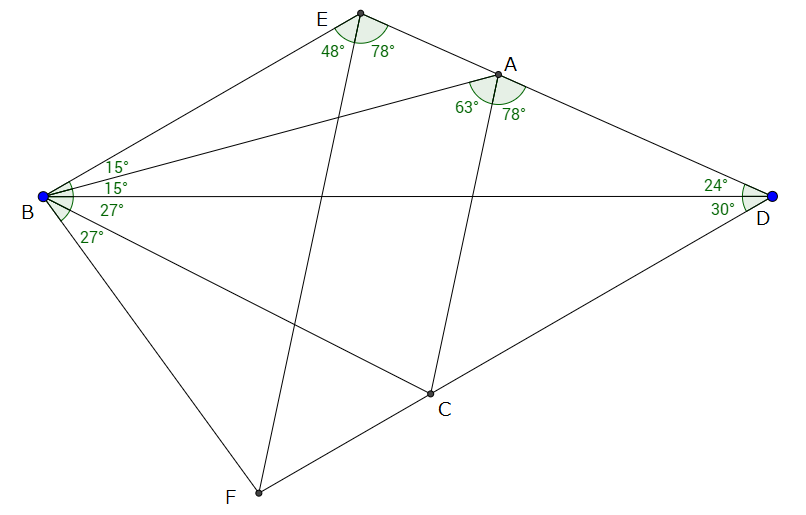
四角形 ${BFDG}$ は平行四辺形なので、 ${DG=BF}$ より、 ${BE=BF}$ です。

ここで角の二等分線定理を使います。
${EA:AD=BE:BD, FC:CD=BF:BD, BE=BF}$ より ${EA:AD=FC:CD}$ なので ${EF//AC}$ となります。
また ${BE=BF}$ より ${\angle BEF=48^\circ}$ 。よって ${\angle DEF=78^\circ}$ です。
${EF//AC}$ より ${\angle DAC =\angle DEF=78^\circ}$ 。
したがって ${\angle BAC=63^\circ}$ となり、これが答えです。