そのあと2週間後に解けた問題である。
なかなか面白かった。
財団が用意していた解答例と違ったので、書く。
問題
鋭角三角形ABCにおいて、垂心をH、外心をOとする。また、Oを通り直線に平行な直線とAB、ACの交点をそれぞれP、Qとし、線分AHの中点をMとする。このとき、∠BMP=∠CMQを示せ。
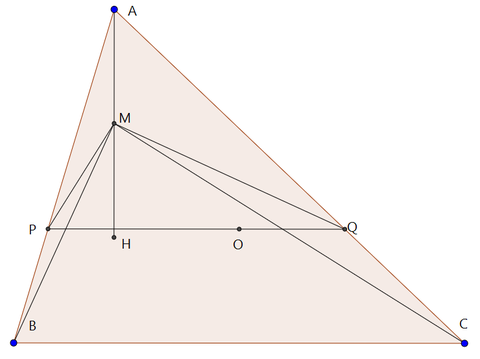
この問題、点PとかQとかMとかいうよくわからない点を
どう扱っていくかが難しい。
これ、実は∠BMQが直角になるのである。
これは図を丁寧に書かないと気付かなさそう。
では、自分の考えた解答。
証明
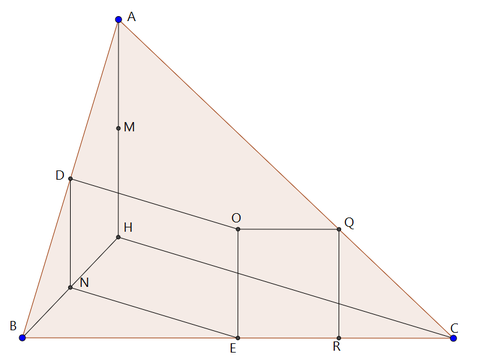
まず,辺AB,BC,BHの中点をそれぞれD,E,Nとする。
そして点Qから辺BCに下した垂線の足をRとする。
このとき,中点連結定理よりDN//AH,
またAH⊥BC,AH⊥OEよりAH//OE
よってDN//OE
同じようにしてEN//OD
ゆえに四角形ODNEは平行四辺形となる。
よってDN=OEが成り立つ。
また四角形OERQは長方形より,OE=QR
そして中点連結定理よりAM=MH=AH/2=DN
したがってAM=MH=QRが成り立つ。
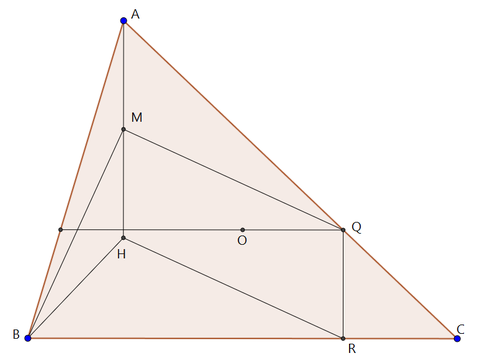
よって四角形AMRQ,MHRQも平行四辺形となるから,
AC//MR,MQ//HRが成り立つ。
ここで△MBRに注目する。
MH⊥BR,またAC//MR,AC⊥BHよりBH⊥MR
が成り立つことから,点Hは△MBRの垂心となる。
よって,RH⊥MBが成り立つ。
したがって,RH//QMより,
MB⊥QMすなわち∠BMQ=90°となる。
∠CMPについても同じことが言える。
したがって∠BMQ=∠CMPとなり,
∠BMP=∠CMQとなることが証明された。
点Hが△MBRの垂心にもなるというところが面白かった。
(図は、GebGebraを使用して作成した。)