三角形ABCにおいて、外接円の半径をR、内接円の半径をrとおくとR≧2rが成り立つ。
というものである。
これの円の反転を使ったきれいな証明を見つけたので、書いておく。
まず次の補題を使う。
補題:半径の等しい3つの円が1点で交わるとき、2つの円が交わる交点3つをとおる円は、元の3つの円の半径に等しい。
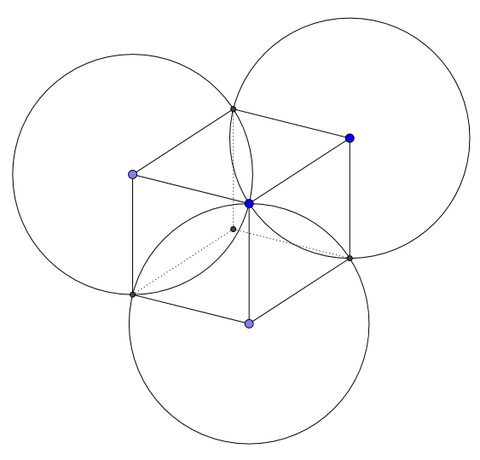
証明は略するが、図にヒントが書かれてあるので、参考にしてほしい。
では本題の証明。
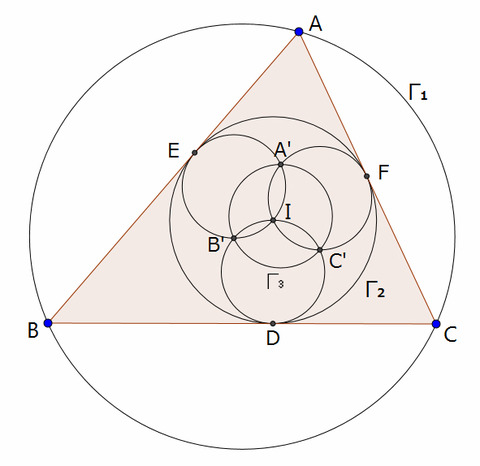
三角形ABCの外接円を\(\Gamma_{1}\)、内接円を\(\Gamma_{2}\)とし、
\(\Gamma_{2}\)と辺BC,CA,ABの接点をそれぞれD,E,Fとする。
このとき\(\Gamma_{2}\)を反転円として辺BC,CA,ABを反転すると、
これらはそれぞれ点Iと点D,E,Fを直径とする円になる。(上図参照)
このとき円どうしの交点を上図のように名前を付けると、
点Aは点A'に、点Bは点B'に、点Cは点C'に対応される。
よって\(\Gamma_{2}\)を反転円として\(\Gamma_{1}\)を反転すると、
点A',B',C'をとおる円になる。
補題よりこの円の半径はr/2である。
これからR≧2rを示すのは割と簡単なので、考えてみてほしい。