等角共役点:三角形ABCと点 P がある。
角の頂点を通る直線 l と角の二等分線に関して対称な直線 m を l の等角共役線という。
AP,BP,CP の等角共役線は一点で交わり,これを P の等角共役点という。
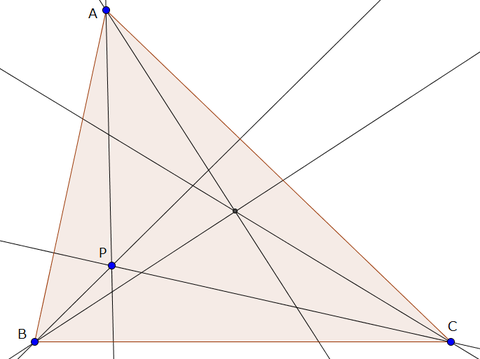
この、「一点で交わる」という部分の証明はいろいろあるのだが、
ここでは先日思いついた証明を書く。
角度を円に対して使うことで、角度を辺の長さとして扱えることを用いた証明だ。
まず次の定理を証明する。
弦に対するチェバの定理
円周上の点A,B,C,D,E,Fに対し、直線AD,BE,CFがどれも点Xをとおるとき、
\[\frac{AB}{BC} \cdot \frac{CD}{DE} \cdot \frac{EF}{FA}=1\]
が成り立つ。
証明
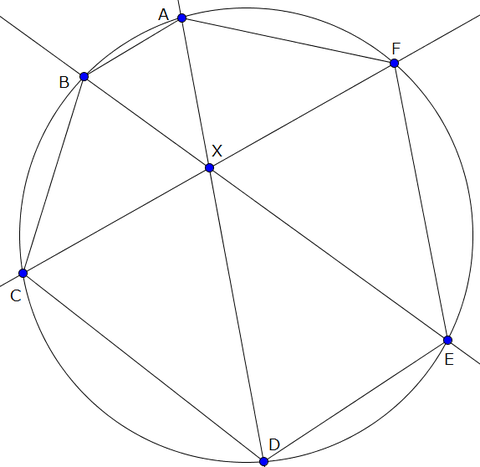
\(\frac{AB}{DE}=\frac{XA}{XE},\frac{BC}{EF}=\frac{XC}{XE},\frac{CD}{FA}=\frac{XC}{XA}\)より
\(\frac{AB}{DE}\cdot \frac{BC}{EF}\cdot \frac{CD}{FA}=\frac{XA}{XE}\cdot \frac{XC}{XE}\cdot \frac{XC}{XA}=1\)
よって\(\frac{AB}{BC} \cdot \frac{CD}{DE} \cdot \frac{EF}{FA}=1\)がなりたつ。
ちなみに、これは逆も成り立つ。
では本題の証明。
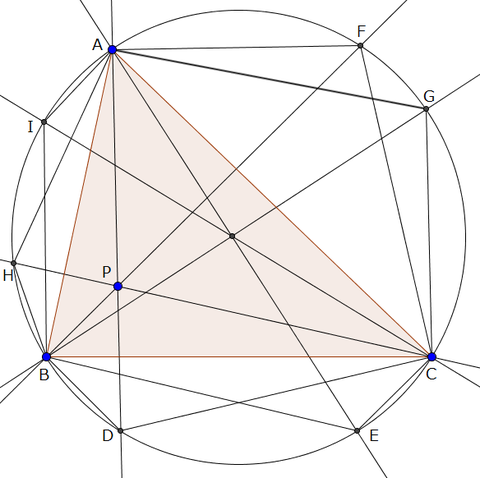
弦に対するチェバの定理より、
\(\frac{BD}{DC} \cdot \frac{CF}{FA} \cdot \frac{AH}{HB}=1\)
また、弦に対する角が等しいからBD=EC,BE=DC,CG=FA,CF=GA,AI=HB,AH=IB
よって\(\frac{EC}{BE} \cdot \frac{GA}{CG} \cdot \frac{IB}{AI}=1\)
チェバの定理の逆より、AP,BP,CP の等角共役線は一点で交わる。□
この定理は意外と有用なので、知っておくべき。