広中杯2016ファイナル3問目

この問題、本番では全然解けず、
しかし家でやってみたら解けてしまったという
悔しい問題。

問題
へこみのない四角形ABCDの対角線ACとBDは点Eにおいて垂直に交わっていて、
∠EBC=12°, ∠EAB=∠CDE=33°, BE+EC=1
となっている。
このとき、△ABEの面積と△CDEの面積の差を求めよ。

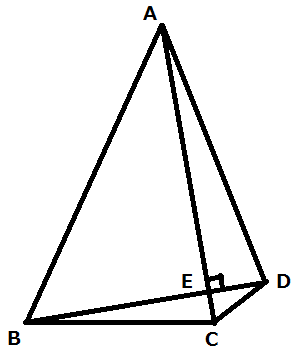
この問題は、BE+EC=1という条件をどのように使うかが難しい。
とある有名問題に結び付けられるか。
（この解き方はほんの一例。）

解答

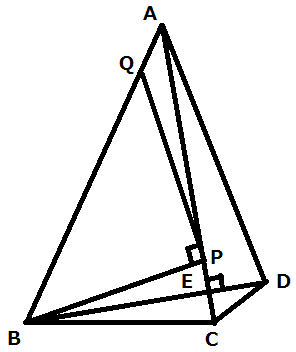
辺BDを軸として点Cに対称な点をPとする。
そして、辺AB上に∠BPQ=90°となる点Qをとる。

このとき、簡単な計算で∠PBQ=45°がわかるので、
△BPQは直角二等辺三角形である。よってBP=PQ。
また、BC=BPより、BC=PQである。

そして、簡単な計算で∠APQ=∠DBC=12°、
∠AQP=∠DCB=135°がなので、
BC=PQとあわせると、△AQP≡△DCBということがわかる。

ここで、△ABEの面積と△CDEの面積の差は
△ABCの面積と△DBCの面積の差に等しく、
それは四角形QBCPの面積に等しい。（△AQP≡△DCBより）

では次に、四角形QBCPの面積を求めるのだが、
これは有名問題の変化形である。

その有名問題というのが、

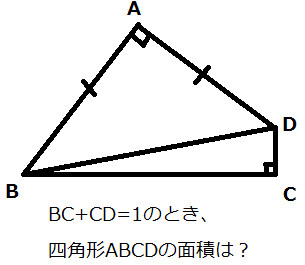
略解はこれ。こたえは1/4である。

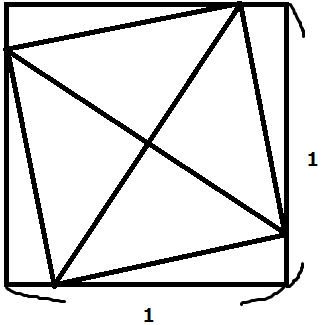
もうわかっただろう。四角形QBCPの面積は、1/2である。
有名問題の図形を2倍にしたものであることがわかるだろう。

というわけで、こたえは1/2である。