お久しぶりです. 約1か月半ぶりの更新でしょうか. 今回の内容は初等幾何です.
曲紹介
たけのこ赤軍さんのブログ
o-v-e-r-h-e-a-t.hatenablog.com
にならい, 曲紹介を.
(続けてほしいかどうかはまた聞きます)
この記事はこの曲を聴きながら読むのがオススメです:
問題
有名な平面幾何の難問として, 次のようなものがあります.
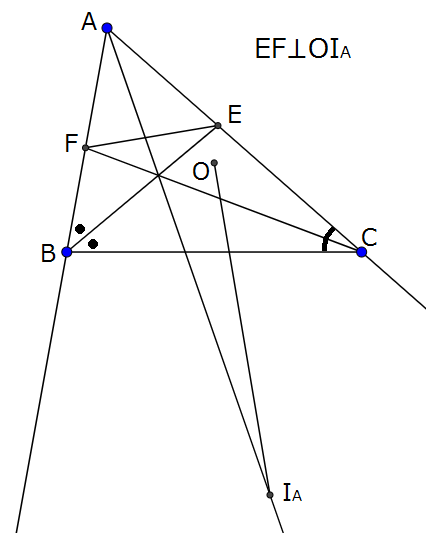
図において, \(O\)は\(\triangle ABC\)の外心, \(I_A\)は角\(A\)内の傍心とする.
このとき, \(EF \perp OI_A\)を証明せよ.
問題自体はシンプルですが, かなりの難問です. まず, 結ぶ線が特殊ですね. 点\(E,F\)を結ぶのは考えづらいし, ましてや外心と傍心を結ぶなんてやばそうです.
僕は, この問題が難しいとうわさで聞いていたので解こうとしたのですが全然わかりませんでした. 手も足も出ないような状況です.
しかし少し時がたち, 何か幾何の問題を作ろうと思っていろいろ図形を描いていったら, たまたまこの問題が解けてしまいました.
今回はその証明を書こうと思っています.
準備
この証明を理解するには, 円による反転の知識(初歩)とオイラー線の知識(初歩)が必要なので, まず解説します.
反転
そもそも反転とは?ということについてはこの記事を見てください.
反転幾何の基礎 | 高校数学の美しい物語
またこのブログでは, この記事の事実2を使います.
円に内接もするし外接もする四角形 - 数学徘徊記
オイラー線
この記事では,
「三角形の外心, 重心, 九点円の中心は同一直線上にある」
という事実を使います. この直線はオイラー線と呼ばれます.
ちょうどいい練習問題なので, 解いてみてください.
オイラー線はこのほかにも垂心などいろいろな点を通りますがここでは使いません.
オイラー線 - Wikipedia
証明
準備が終わったので, 証明に移りましょう. 証明は主に3ステップです.
まず, 直線\(OI_A\)がある三角形のオイラー線になることを示します.
つぎに, 点\(O\)から直線\(EF\)に下した垂線の足を\(H\)とし, \(HI_A\)が同じオイラー線となることを示します.
最後に, \(EF\perp OI_A\)を示します.
※注意
多少の行間がありますが, どれもそんなに難しくないようにしています.
ステップ1

\(I_A\)を中心とする\(\triangle ABC\)の傍心を\(\Gamma\)とおきます. ここから, 対象\(X\)を円\(\Gamma\)に対して反転させたものを\(X'\)と表すことにします. また, これからは円\(\Gamma\)でしか反転しないので, 「円\(\Gamma\)で」という言葉を省略します.
\(\triangle ABC\)の外接円\(\Omega\)を反転させてみましょう(これを\(\Omega'\)とする). すると\(\triangle A'B'C'\)の外接円となります.
点\(A',B',C'\)はそれぞれ辺の中点となるので, \(\Omega'\)は\(\triangle PQR\)の九点円となります.
\(\Omega'\)の中心を\(N\)とすると, 点\(O,N,I_A\)が同一直線上にあることはすぐわかります(円の対称性)(点\(O\)は反転で点\(N\)に移されることではないのに注意).
また, \(I_A\)は\(\triangle PQR\)にとって外心となるため, 直線\(OI_A\)は\(\triangle PQR\)のオイラー線となります.
ステップ2

点\(O\)から直線\(EF\)に下した垂線の足を\(H\)とします.
ここで, \(EI_A\)を直径とする円を\(\omega_1\), \(FI_A\)を直径とする円を\(\omega_2\)とすると, これらは点\(H\)を通ります. すなわち, 点\(H\)は\(\omega_1\)と\(\omega_2\)の交点の一つと考えられます.
また\(\angle EBI_A=\angle EQI_A=\angle FCI_A=\angle FRI_A=90^\circ \)より, \(\omega_1\)は点\(B,Q\)を, \(\omega_2\)は点\(C,R\)を通ります.
\(\omega_1, \omega_2\)を反転させてみましょう. これらは点\(I_A\)(反転の中心)を通るので, 反転させたら直線となります.
また点\(B,C\)は反転させると点\(B',C'\)に移り, また点\(Q,R\)は円\(\Gamma\)上にあるため反転しても動きません. そのため, \(\omega_1, \omega_2\)はそれぞれ直線\(B'Q,C'R\)に移ります.
直線\(B'Q,C'R\)は\(\triangle PQR\)にとって中線となるため, それらの交点を\(G\)とおくと, \(G\)は\(\triangle PQR\)の重心となります.
点\(H\)は反転すると点\(G\)に移るため, 点\(H,G,I_A\)は同一直線上にあります. 直線\(GI_A\)は\(\triangle PQR\)にとってオイラー線となるので, 直線\(HI_A\)は\(\triangle PQR\)のオイラー線となります.
ステップ3
ここまでできれば後は簡単です. 定義より\(EF\perp OH\)であり, また直線\(OH\)と\(OI_A\)はどちらも\(\triangle PQR\)のオイラー線となるから一致するので, \(EF\perp OI_A\)が示されました.