三角形\(ABC\)の外心を\(O\)とし、辺\(BC,CA,AB\)の中点をそれぞれ\(M_A,M_B,M_C\)とする。
円に関する反転を用いた解法です。
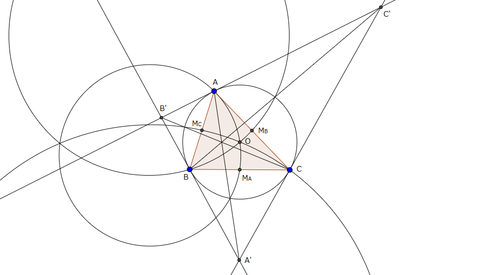
点\(M_A,M_B,M_C\)をそれぞれ三角形\(ABC\)の外接円で反転させます。
このとき、点\(M_A,M_B,M_C\)はそれぞれ図の点\(A',B',C'\)に移ります。
(点\(A',B',C'\)は、直線\(B'C',C'A',A'B'\)がそれぞれ点\(A,B,C\)で三角形\(ABC\)の外接円に接するような点)
なぜなら、たとえば\(M_A\)に注目するとき、
\(\angle OM_AB=\angle OAB\)より\(\triangle OM_AB\simeq \triangle OAB\)だから
\(OM_A\cdot OA'=OB^2\)となるからです。 \(M_A,M_B\)についても同様です。
よって、三角形\(AOM_A,BOM_B,COM_C\)の外接円は、反転によって
それぞれ直線\(AA',BB'CC'\)に移ります。
そして、
\[\frac{A'B}{BB'} \cdot \frac{B'A}{AC'} \cdot \frac{C'C}{CA'} = 1\]
であるので、チェバの定理の逆により、この3つの直線は1点で交わります。
よって、反転する前の元の図形、三角形\(AOM_A,BOM_B,COM_C\)の外接円は1点で交わります。

点\(M_A,M_B,M_C\)をそれぞれ三角形\(ABC\)の外接円で反転させます。
このとき、点\(M_A,M_B,M_C\)はそれぞれ図の点\(A',B',C'\)に移ります。
(点\(A',B',C'\)は、直線\(B'C',C'A',A'B'\)がそれぞれ点\(A,B,C\)で三角形\(ABC\)の外接円に接するような点)
なぜなら、たとえば\(M_A\)に注目するとき、
\(\angle OM_AB=\angle OAB\)より\(\triangle OM_AB\simeq \triangle OAB\)だから
\(OM_A\cdot OA'=OB^2\)となるからです。 \(M_A,M_B\)についても同様です。
よって、三角形\(AOM_A,BOM_B,COM_C\)の外接円は、反転によって
それぞれ直線\(AA',BB'CC'\)に移ります。
そして、
\[\frac{A'B}{BB'} \cdot \frac{B'A}{AC'} \cdot \frac{C'C}{CA'} = 1\]
であるので、チェバの定理の逆により、この3つの直線は1点で交わります。
よって、反転する前の元の図形、三角形\(AOM_A,BOM_B,COM_C\)の外接円は1点で交わります。
