広中杯2016トライアル受けてきた。
ファイナルは用事があるため残念ながらいけない。
問題を公表するのはなんかモラルに反しそうなので、やめておく。
I-(1)
「クマモトガンバレ」の文字が。問題作成者の声が聞こえた。
場合分けすれば簡単。
I-(2)
「1以下」を見落とすという大失態。
I-(3)
面積を使えば割と簡単に求められる。
(追記:ひどいうっかりミスをした)
I-(4)
え!?自明じゃない?
I-(5)
くっそめんどくさそうなので、6!=720と書いたが、間違っているのだろうか。
II-(1)
なんだこの条件は!?さすがに汚いだろ!?
しかし条件に近づけるようにして式変形させて解いた。
II-(2)
ひらめきが肝心。終了10分前にひらめいた。
II-(3)
まためんどくさそうな問題。整数論だから解きたいなと。
自信のない解答を書いた。
II-(4)
これもめんどくさそう。やってない。
問題3
これも白紙。
点数はどうなるのか…。
追記(6/14)
解答が発表された。
本当にうっかりミスが痛い。
等角共役点の証明
等角共役点とはこのようなものだ。
等角共役点:三角形ABCと点 P がある。
角の頂点を通る直線 l と角の二等分線に関して対称な直線 m を l の等角共役線という。
AP,BP,CP の等角共役線は一点で交わり,これを P の等角共役点という。
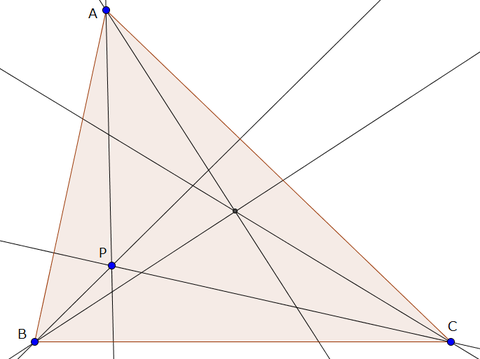
この、「一点で交わる」という部分の証明はいろいろあるのだが、
ここでは先日思いついた証明を書く。
角度を円に対して使うことで、角度を辺の長さとして扱えることを用いた証明だ。
まず次の定理を証明する。
弦に対するチェバの定理
円周上の点A,B,C,D,E,Fに対し、直線AD,BE,CFがどれも点Xをとおるとき、
\[\frac{AB}{BC} \cdot \frac{CD}{DE} \cdot \frac{EF}{FA}=1\]
が成り立つ。
証明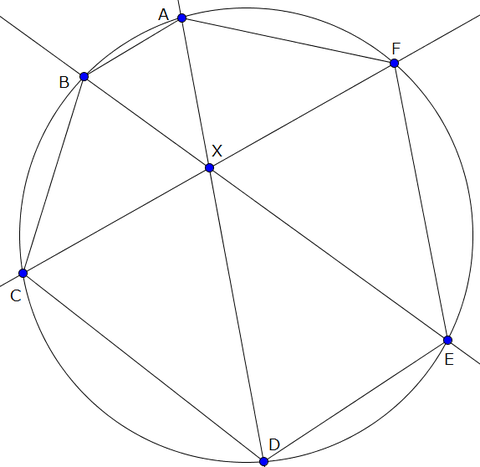
\(\frac{AB}{DE}=\frac{XA}{XE},\frac{BC}{EF}=\frac{XC}{XE},\frac{CD}{FA}=\frac{XC}{XA}\)より
\(\frac{AB}{DE}\cdot \frac{BC}{EF}\cdot \frac{CD}{FA}=\frac{XA}{XE}\cdot \frac{XC}{XE}\cdot \frac{XC}{XA}=1\)
よって\(\frac{AB}{BC} \cdot \frac{CD}{DE} \cdot \frac{EF}{FA}=1\)がなりたつ。
ちなみに、これは逆も成り立つ。
では本題の証明。
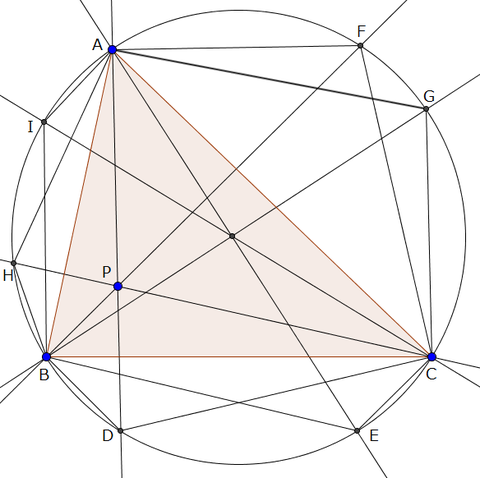
弦に対するチェバの定理より、
\(\frac{BD}{DC} \cdot \frac{CF}{FA} \cdot \frac{AH}{HB}=1\)
また、弦に対する角が等しいからBD=EC,BE=DC,CG=FA,CF=GA,AI=HB,AH=IB
よって\(\frac{EC}{BE} \cdot \frac{GA}{CG} \cdot \frac{IB}{AI}=1\)
チェバの定理の逆より、AP,BP,CP の等角共役線は一点で交わる。□
この定理は意外と有用なので、知っておくべき。
等角共役点:三角形ABCと点 P がある。
角の頂点を通る直線 l と角の二等分線に関して対称な直線 m を l の等角共役線という。
AP,BP,CP の等角共役線は一点で交わり,これを P の等角共役点という。

この、「一点で交わる」という部分の証明はいろいろあるのだが、
ここでは先日思いついた証明を書く。
角度を円に対して使うことで、角度を辺の長さとして扱えることを用いた証明だ。
まず次の定理を証明する。
弦に対するチェバの定理
円周上の点A,B,C,D,E,Fに対し、直線AD,BE,CFがどれも点Xをとおるとき、
\[\frac{AB}{BC} \cdot \frac{CD}{DE} \cdot \frac{EF}{FA}=1\]
が成り立つ。
証明

\(\frac{AB}{DE}=\frac{XA}{XE},\frac{BC}{EF}=\frac{XC}{XE},\frac{CD}{FA}=\frac{XC}{XA}\)より
\(\frac{AB}{DE}\cdot \frac{BC}{EF}\cdot \frac{CD}{FA}=\frac{XA}{XE}\cdot \frac{XC}{XE}\cdot \frac{XC}{XA}=1\)
よって\(\frac{AB}{BC} \cdot \frac{CD}{DE} \cdot \frac{EF}{FA}=1\)がなりたつ。
ちなみに、これは逆も成り立つ。
では本題の証明。

弦に対するチェバの定理より、
\(\frac{BD}{DC} \cdot \frac{CF}{FA} \cdot \frac{AH}{HB}=1\)
また、弦に対する角が等しいからBD=EC,BE=DC,CG=FA,CF=GA,AI=HB,AH=IB
よって\(\frac{EC}{BE} \cdot \frac{GA}{CG} \cdot \frac{IB}{AI}=1\)
チェバの定理の逆より、AP,BP,CP の等角共役線は一点で交わる。□
この定理は意外と有用なので、知っておくべき。
円の反転とオイラーの不等式
オイラーの不等式とは、
三角形ABCにおいて、外接円の半径をR、内接円の半径をrとおくとR≧2rが成り立つ。
というものである。
これの円の反転を使ったきれいな証明を見つけたので、書いておく。
まず次の補題を使う。
補題:半径の等しい3つの円が1点で交わるとき、2つの円が交わる交点3つをとおる円は、元の3つの円の半径に等しい。
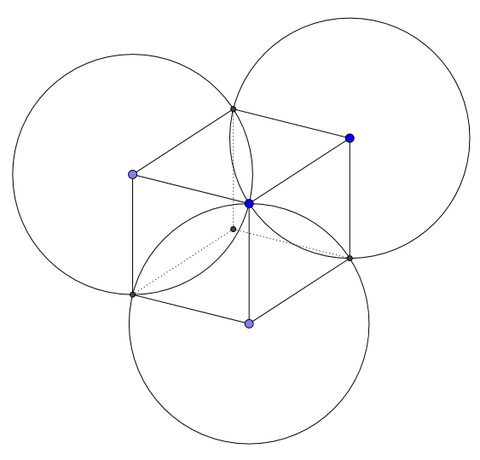
証明は略するが、図にヒントが書かれてあるので、参考にしてほしい。
では本題の証明。
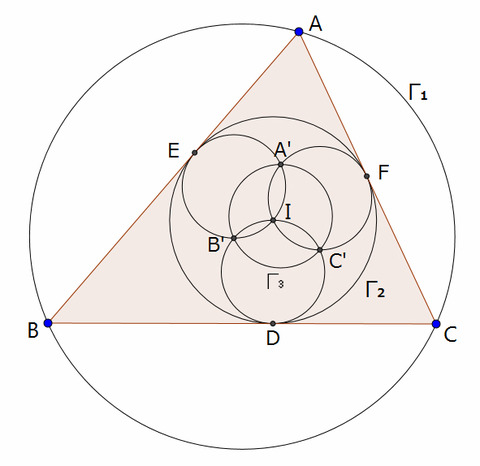
三角形ABCの外接円を\(\Gamma_{1}\)、内接円を\(\Gamma_{2}\)とし、
\(\Gamma_{2}\)と辺BC,CA,ABの接点をそれぞれD,E,Fとする。
このとき\(\Gamma_{2}\)を反転円として辺BC,CA,ABを反転すると、
これらはそれぞれ点Iと点D,E,Fを直径とする円になる。(上図参照)
このとき円どうしの交点を上図のように名前を付けると、
点Aは点A'に、点Bは点B'に、点Cは点C'に対応される。
よって\(\Gamma_{2}\)を反転円として\(\Gamma_{1}\)を反転すると、
点A',B',C'をとおる円になる。
補題よりこの円の半径はr/2である。
これからR≧2rを示すのは割と簡単なので、考えてみてほしい。
三角形ABCにおいて、外接円の半径をR、内接円の半径をrとおくとR≧2rが成り立つ。
というものである。
これの円の反転を使ったきれいな証明を見つけたので、書いておく。
まず次の補題を使う。
補題:半径の等しい3つの円が1点で交わるとき、2つの円が交わる交点3つをとおる円は、元の3つの円の半径に等しい。

証明は略するが、図にヒントが書かれてあるので、参考にしてほしい。
では本題の証明。

三角形ABCの外接円を\(\Gamma_{1}\)、内接円を\(\Gamma_{2}\)とし、
\(\Gamma_{2}\)と辺BC,CA,ABの接点をそれぞれD,E,Fとする。
このとき\(\Gamma_{2}\)を反転円として辺BC,CA,ABを反転すると、
これらはそれぞれ点Iと点D,E,Fを直径とする円になる。(上図参照)
このとき円どうしの交点を上図のように名前を付けると、
点Aは点A'に、点Bは点B'に、点Cは点C'に対応される。
よって\(\Gamma_{2}\)を反転円として\(\Gamma_{1}\)を反転すると、
点A',B',C'をとおる円になる。
補題よりこの円の半径はr/2である。
これからR≧2rを示すのは割と簡単なので、考えてみてほしい。
ハフマン符号をExcelでやってみる
最近「なんでファイルが圧縮できるんだ?」って思ったので、
Wikipediaでいろいろ調べてみると、
「ハフマン符号」というものがあった。
ハフマン符号 - Wikipedia
どういうものかは上の記事を見てもらえばわかる。
やはり自分は
「Excelでやってみたいなあ」
と思った。
しかしコードを組んでいったところ
バグが大量発生し本当に大変だった。
どんなアルゴリズムでやったのかをまず説明する。
まず1と0からできた文字を、4けたごとに区切ってまとめる(つまり16進法にする)。
そうすると0から15までの整数の数列になる。
そして、0はいくつか、1はいくつか…と、0から15までの整数が
それぞれいくつあるかをカウントする。
まあここまでは下ごしらえだ。
そしてここからハフマン符号をつけていくのだが、
これが意外とプログラムを組むのがムズい。
ハフマン符号のつけ方はWikiに書いてあるが、これを実装するのがきつかった。
努力の結果、VBAソースコードが出来上がった。
ソースコード
バグが次から次へとあらわれたので、意外と時間がかかった。
Excelファイルも上げておく。
HuffmanCording.xlsm
前述のとおりこれは圧縮するために用いるものだ。
このファイルでいろいろ実験してみると、
0と1の偏りが大きい場合によく圧縮されるということが分かった。
Wikipediaでいろいろ調べてみると、
「ハフマン符号」というものがあった。
ハフマン符号 - Wikipedia
どういうものかは上の記事を見てもらえばわかる。
やはり自分は
「Excelでやってみたいなあ」
と思った。
しかしコードを組んでいったところ
バグが大量発生し本当に大変だった。
どんなアルゴリズムでやったのかをまず説明する。
まず1と0からできた文字を、4けたごとに区切ってまとめる(つまり16進法にする)。
そうすると0から15までの整数の数列になる。
そして、0はいくつか、1はいくつか…と、0から15までの整数が
それぞれいくつあるかをカウントする。
まあここまでは下ごしらえだ。
そしてここからハフマン符号をつけていくのだが、
これが意外とプログラムを組むのがムズい。
ハフマン符号のつけ方はWikiに書いてあるが、これを実装するのがきつかった。
努力の結果、VBAソースコードが出来上がった。
ソースコード
バグが次から次へとあらわれたので、意外と時間がかかった。
Excelファイルも上げておく。
HuffmanCording.xlsm
前述のとおりこれは圧縮するために用いるものだ。
このファイルでいろいろ実験してみると、
0と1の偏りが大きい場合によく圧縮されるということが分かった。
2015ジュニア広中杯の問題について
2015年ジュニア広中杯の問題4番。
答えを言ってしまうと、最少は155155(=2015x77)、次は179335(=2015x89)である。
この問題、桁数を8桁までとしても252個あるので、
答えはものすごくたくさんあり、いい問題とは言えない。
しかしこのように一般化して考えるとおもしろい。
この問題の回答では、任意の奇数nの倍数で、どの桁の数字も奇数であるものの上界が
低ければ低い解答ほど、なおよいのだが。
まあ考えてみよう。
実はこの問題、問題文で「奇数」を「偶数」と変えた問題のほうは簡単である。
2k以下の任意の自然数nの倍数で、k桁以下でどの桁の数字も偶数であるものが存在することが簡単に示せる。
たとえばk=2の場合、次のような数の集合を考える。
{88,68,66,46,44,24,22,2,0}
鳩ノ巣原理より、nのあまりは9個あるので互いに等しいものが存在する。
その2つの差をとればnの倍数となるが、これはどの桁の数字も偶数である。
よって示せた。この方法はkがどのような値でも使える。
しかし奇数で同じ方法を使おうとすると、うまくいかない。
5の倍数でないのなら、
1,11,111,…のなかに必ずnの倍数はあるのだが、
5の倍数のときもうまくいくうまい方法はあるのか…。
一応数表作ってみた。
数表
何かわかったらコメントお願いします。
2015の倍数で、どの桁の数字も奇数であるものを一つ求めよ。ただし、12桁以内のものに限る。という問題があった。
答えを言ってしまうと、最少は155155(=2015x77)、次は179335(=2015x89)である。
この問題、桁数を8桁までとしても252個あるので、
答えはものすごくたくさんあり、いい問題とは言えない。
しかしこのように一般化して考えるとおもしろい。
任意の奇数nの倍数で、どの桁の数字も奇数であるものは存在するか?
この問題の回答では、任意の奇数nの倍数で、どの桁の数字も奇数であるものの上界が
低ければ低い解答ほど、なおよいのだが。
まあ考えてみよう。
実はこの問題、問題文で「奇数」を「偶数」と変えた問題のほうは簡単である。
2k以下の任意の自然数nの倍数で、k桁以下でどの桁の数字も偶数であるものが存在することが簡単に示せる。
たとえばk=2の場合、次のような数の集合を考える。
{88,68,66,46,44,24,22,2,0}
鳩ノ巣原理より、nのあまりは9個あるので互いに等しいものが存在する。
その2つの差をとればnの倍数となるが、これはどの桁の数字も偶数である。
よって示せた。この方法はkがどのような値でも使える。
しかし奇数で同じ方法を使おうとすると、うまくいかない。
5の倍数でないのなら、
1,11,111,…のなかに必ずnの倍数はあるのだが、
5の倍数のときもうまくいくうまい方法はあるのか…。
一応数表作ってみた。
数表
何かわかったらコメントお願いします。
昔、線を引いて遊んだこと。
初めての代数編。
昔、こんな感じで線を引いて遊んだことがあるのだが…。
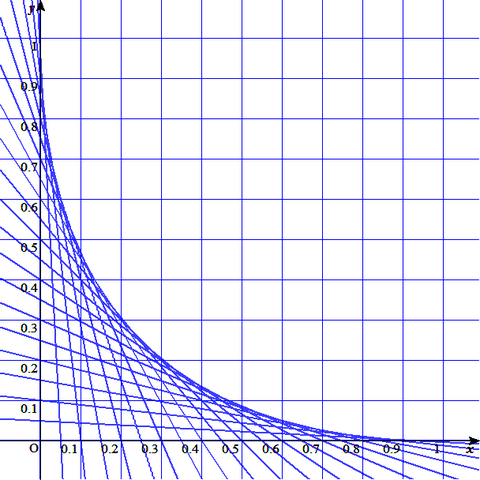
0と1、0.1と0.9、0.2と0.8、…と線を結んでいくと、なんだか曲線が見えてくる。
直線が曲線を作るのは、かなり不思議である。
で、中1の時にこんなことが疑問に思った。
「この曲線はどのような式であらわされるのだろう?」
当時、微分っぽいことをするのはわかったが、具体的な求め方はわからなかった。
それから6か月後解けたので、その方法を紹介する。
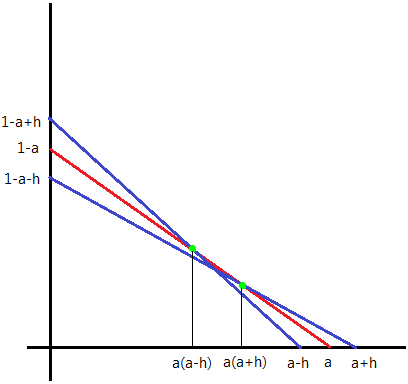
あの曲線とそれを作っている任意の直線は接すると考えていい。
まず0<a<1を満たす実数aについて、
直線 \(y=-\frac{1-a}{a}x+1-a\) と \(y=-\frac{1-a-h}{a+h}x+1-a-h\) の交点を計算すると、
計算はめんどくさいが、x座標がa(a+h)のとき2直線が交わることがわかる。
同じように、直線 \(y=-\frac{1-a}{a}x+1-a\) と \(y=-\frac{1-a+h}{a-h}x+1-a+h\) の交点を計算することで
x座標がa(a-h)のとき2直線が交わることがわかる。
このhをだんだんと小さくすることで、この2つの交点はそれぞれ
だんだんとx座標が\(a^2\)に近くなっていく。
この近づいた点があの曲線との接線となるので、
任意の直線\(y=-\frac{1-a}{a}x+1-a\)とあの曲線は
x座標が\(a^2\)の点で接すると考えていい。
\(y=-\frac{1-a}{a}x+1-a\)に\(x=a^2\)を代入することで、
点\((a^2,(1-a)^2)\)があの曲線を通るということがわかる。
\(x=a^2,y=(1-a)^2\)でaが0~1の値を動くときのグラフは、
\(\sqrt{x}+\sqrt{y}=1\)のグラフに等しい。
よってこの曲線は\(\sqrt{x}+\sqrt{y}=1\)である。
ちなみにこれは放物線である。(行列変換で\(\frac{\pi}{4}\)回転させるとわかる。)
この曲線が放物線になるのは意外だった。
Wikipediaによると、これは「包絡線」というらしい。
包絡線 - Wikipedia
昔、こんな感じで線を引いて遊んだことがあるのだが…。

0と1、0.1と0.9、0.2と0.8、…と線を結んでいくと、なんだか曲線が見えてくる。
直線が曲線を作るのは、かなり不思議である。
で、中1の時にこんなことが疑問に思った。
「この曲線はどのような式であらわされるのだろう?」
当時、微分っぽいことをするのはわかったが、具体的な求め方はわからなかった。
それから6か月後解けたので、その方法を紹介する。

あの曲線とそれを作っている任意の直線は接すると考えていい。
まず0<a<1を満たす実数aについて、
直線 \(y=-\frac{1-a}{a}x+1-a\) と \(y=-\frac{1-a-h}{a+h}x+1-a-h\) の交点を計算すると、
計算はめんどくさいが、x座標がa(a+h)のとき2直線が交わることがわかる。
同じように、直線 \(y=-\frac{1-a}{a}x+1-a\) と \(y=-\frac{1-a+h}{a-h}x+1-a+h\) の交点を計算することで
x座標がa(a-h)のとき2直線が交わることがわかる。
このhをだんだんと小さくすることで、この2つの交点はそれぞれ
だんだんとx座標が\(a^2\)に近くなっていく。
この近づいた点があの曲線との接線となるので、
任意の直線\(y=-\frac{1-a}{a}x+1-a\)とあの曲線は
x座標が\(a^2\)の点で接すると考えていい。
\(y=-\frac{1-a}{a}x+1-a\)に\(x=a^2\)を代入することで、
点\((a^2,(1-a)^2)\)があの曲線を通るということがわかる。
\(x=a^2,y=(1-a)^2\)でaが0~1の値を動くときのグラフは、
\(\sqrt{x}+\sqrt{y}=1\)のグラフに等しい。
よってこの曲線は\(\sqrt{x}+\sqrt{y}=1\)である。
ちなみにこれは放物線である。(行列変換で\(\frac{\pi}{4}\)回転させるとわかる。)
この曲線が放物線になるのは意外だった。
Wikipediaによると、これは「包絡線」というらしい。
包絡線 - Wikipedia
2016JJMO本選第4問
これは本番中全然解けなかったものの、
そのあと2週間後に解けた問題である。
なかなか面白かった。
財団が用意していた解答例と違ったので、書く。
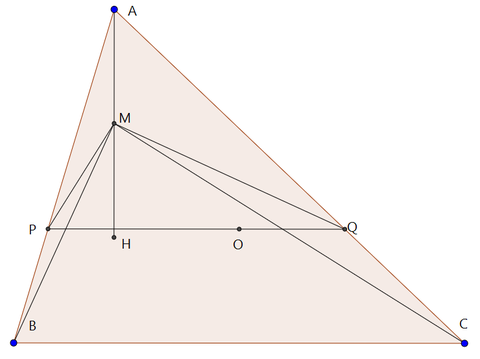
この問題、点PとかQとかMとかいうよくわからない点を
どう扱っていくかが難しい。
これ、実は∠BMQが直角になるのである。
これは図を丁寧に書かないと気付かなさそう。
では、自分の考えた解答。
証明
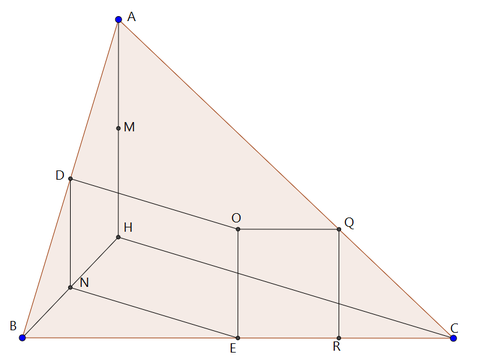
まず,辺AB,BC,BHの中点をそれぞれD,E,Nとする。
そして点Qから辺BCに下した垂線の足をRとする。
このとき,中点連結定理よりDN//AH,
またAH⊥BC,AH⊥OEよりAH//OE
よってDN//OE
同じようにしてEN//OD
ゆえに四角形ODNEは平行四辺形となる。
よってDN=OEが成り立つ。
また四角形OERQは長方形より,OE=QR
そして中点連結定理よりAM=MH=AH/2=DN
したがってAM=MH=QRが成り立つ。
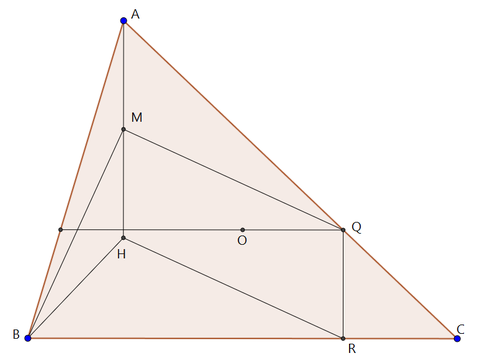
よって四角形AMRQ,MHRQも平行四辺形となるから,
AC//MR,MQ//HRが成り立つ。
ここで△MBRに注目する。
MH⊥BR,またAC//MR,AC⊥BHよりBH⊥MR
が成り立つことから,点Hは△MBRの垂心となる。
よって,RH⊥MBが成り立つ。
したがって,RH//QMより,
MB⊥QMすなわち∠BMQ=90°となる。
∠CMPについても同じことが言える。
したがって∠BMQ=∠CMPとなり,
∠BMP=∠CMQとなることが証明された。
点Hが△MBRの垂心にもなるというところが面白かった。
(図は、GebGebraを使用して作成した。)
そのあと2週間後に解けた問題である。
なかなか面白かった。
財団が用意していた解答例と違ったので、書く。
問題
鋭角三角形ABCにおいて、垂心をH、外心をOとする。また、Oを通り直線に平行な直線とAB、ACの交点をそれぞれP、Qとし、線分AHの中点をMとする。このとき、∠BMP=∠CMQを示せ。

この問題、点PとかQとかMとかいうよくわからない点を
どう扱っていくかが難しい。
これ、実は∠BMQが直角になるのである。
これは図を丁寧に書かないと気付かなさそう。
では、自分の考えた解答。
証明

まず,辺AB,BC,BHの中点をそれぞれD,E,Nとする。
そして点Qから辺BCに下した垂線の足をRとする。
このとき,中点連結定理よりDN//AH,
またAH⊥BC,AH⊥OEよりAH//OE
よってDN//OE
同じようにしてEN//OD
ゆえに四角形ODNEは平行四辺形となる。
よってDN=OEが成り立つ。
また四角形OERQは長方形より,OE=QR
そして中点連結定理よりAM=MH=AH/2=DN
したがってAM=MH=QRが成り立つ。

よって四角形AMRQ,MHRQも平行四辺形となるから,
AC//MR,MQ//HRが成り立つ。
ここで△MBRに注目する。
MH⊥BR,またAC//MR,AC⊥BHよりBH⊥MR
が成り立つことから,点Hは△MBRの垂心となる。
よって,RH⊥MBが成り立つ。
したがって,RH//QMより,
MB⊥QMすなわち∠BMQ=90°となる。
∠CMPについても同じことが言える。
したがって∠BMQ=∠CMPとなり,
∠BMP=∠CMQとなることが証明された。
点Hが△MBRの垂心にもなるというところが面白かった。
(図は、GebGebraを使用して作成した。)