やはり数学好きとしてはジュニア数学オリンピック (JJMO) を受けておきたい。
まだ中2なので、入賞すれば上出来、そうでなくても予選通過はしたいと思って臨んだ。
予選問題は、下記のリンクから。
http://www.imojp.org/challenge/old/jjmo14yq.html
予選は割とよくできた。
ちょうど当日の調子が良く、ノーミスで、予選を通過できた。
予選対策として色々な問題を解いていた甲斐もあった。
今回は図形の問題がやや難しかったと思う。
本選問題は、下記のリンクから。
http://www.imojp.org/challenge/old/jjmo14mq.html
本選前、考えていた構想としては
開始から
1時間 すべての問題をかじってみる
45分 一番解けそうな問題を解く
1時間 次に解けそうな問題を解く
1時間15分 その次に解けそうな問題を解く
というリズムで3問完答すればカンペキ、
でなくても2問は完答、1問はいいところまで解きたいと思っていた。
そして本番。問題をざっとかじってみたところ
問1は点M,P,Qが扱いづらく、1問目にしては難しいなあ、と。
問2は小さい場合に考えて、何となくはわかった。
問3は変数が4つもあるのがきつそうだ。
問4は点Mと点P、点Mと点Qを結ぶのをどう扱えばいいのかが全然わからない。
問5は、空港会社が2種類あると言うのがきつい。
という感じだった。
しかも、得意な整数論がない。
というわけで、まずは問2の解答を書いてみようとしたが、書き方が難しい。
順に斜めに書くことをどうやってきちんと説明するのかということに時間を使ってしまった。
何回も書いては消し、表現を変えていった結果、想像以上に時間を食った。
しかし、なんとか45分くらいで終わらせることが出来た。
次に問1を。
図をそんなに丁寧に書かなかったせいで、
線分PQと線分BCが平行であることに気づかなかった。
(というか計算で初めて気づいた。)
気づくのにかなり時間をとられ、30分ロス。
残り45分くらいになってしまった。
では残り45分の中、問3を解こうかと思ったが、
式を展開しても複雑なのには変わりがなく、手のつけようがなかった。
これはむりかと問4の方に手を出したが、
∠BMPをどのように移せばよいかということが全然わからなかった。
問5はもはやバケモノ。
というわけで、ここは部分点の取りやすそうな問4を解いてみることにした。
しかし45分は有効に使えず、
「辺AB、ACの中点をそれぞれ点D、Eとおくと、
四角形MDOEは平行四辺形になる」
ということしか書けなかった。
全体的に、良くできなかった。(といっても過去問を解いていつもこう)
教訓として、
「コンパス必須!図を丁寧に書き、予想をたてるべし」
である。
図を丁寧に書かなかったせいで、時間をロスした。
また、問4も図を丁寧に書けば発見があったろうに…。
問題コーナー(第1回)解答
この問題は意外な答えになります。
1:正弦定理による解答
△PBA∽△ABCより
\(\cfrac{BC}{\sin(\angle BAC)}=\cfrac{BA}{\sin(\angle BCA)}\)
\(\sin(\angle BAC)=\cfrac{1+\sqrt{5}}{4}\)
2:初等幾何による解答
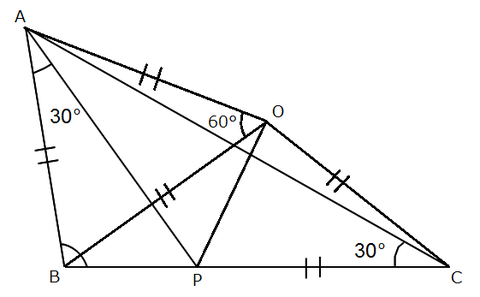
問題
三角形ABCがある。辺BC上にAB=PCとなる点Pを取ったところ、角PAB=角ACBとなった。
このとき、角ABCを求めよ。ただし角ABCは鈍角(90度より大きい)とする。
1:正弦定理による解答
△PBA∽△ABCより
BP:BA=BA:(BP+PC),BP(BP+PC)=BA^2
またBA=PCより、BC=\(\cfrac{1+\sqrt{5}}{2}BA\)
これを使うと、正弦定理より
\(\cfrac{BC}{\sin(\angle BAC)}=\cfrac{BA}{\sin(\angle BCA)}\)
\(\cfrac{\frac{1+\sqrt{5}}{2}BA}{\sin(\angle BAC)}=\cfrac{BA}{\frac{1}{2}}\)
\(\sin(\angle BAC)=\cfrac{1+\sqrt{5}}{4}\)
ここから、何とかして∠BAC=54°と求め、∠ABC=96°と求める。
2:初等幾何による解答

△ABCの外心をOとすると、
AO=BO=CO、また∠AOB=2∠ACB=60°
よって△AOBは正三角形で、AB=PC=AO=BO=CO
そして、△ABPと△AOPにおいて
共通よりAP=AP…①、△AOBは正三角形よりAB=AO…②
また∠BAP=30°、∠OAP=∠OAB-∠BAP=30°より
∠BAP=∠OAP…③
①,②,③より△ABP≡△AOP、BP=OP
ここで∠OBP=θとおくと
∠BOP=θ,∠OPC=2θ,∠POC=2θ,∠OCP=θより
5θ=180°,θ=36°
問題コーナー 第1回(追加)
問題コーナー第1回、正直、正弦定理で余裕に解けると思っていませんか?実際そうなんですが…。
実は、この問題は初等幾何でも解けるんです!
考えてみてください!
実は、この問題は初等幾何でも解けるんです!
考えてみてください!
問題コーナー 第1回
問題コーナーを作りました。
記念すべき第1回なので、自作の問題(自分では良問と思っている)を載せます。
問題
三角形ABCがある。辺BC上にAB=PCとなる点Pを取ったところ、角PAB=角ACBとなった。
このとき、角ABCを求めよ。ただし角ABCは鈍角(90度より大きい)とする。

解答はコメント欄にてお願いします。(コメントするにはこの記事の右上の「Comment」をクリック)
(解答は答えだけでも構いませんが、解き方、感想を書いていただけると嬉しいです。)
解答期限は12月25日まで、正解者発表&解説は12月31日です。
解答欄(コメント欄)にリンクを載せても構いません。
※注意
解答は1人1回しかできません。
2回目以降の回答はお断りします。
また、解答後すぐにはコメントが反映されません。
(反映されると答えが見えてしまうため)
ご了承ください。
解答受付は終了しました
記念すべき第1回なので、自作の問題(自分では良問と思っている)を載せます。
問題
三角形ABCがある。辺BC上にAB=PCとなる点Pを取ったところ、角PAB=角ACBとなった。
このとき、角ABCを求めよ。ただし角ABCは鈍角(90度より大きい)とする。
解答はコメント欄にてお願いします。(コメントするにはこの記事の右上の「Comment」をクリック)
(解答は答えだけでも構いませんが、解き方、感想を書いていただけると嬉しいです。)
解答期限は12月25日まで、正解者発表&解説は12月31日です。
解答欄(コメント欄)にリンクを載せても構いません。
※注意
解答は1人1回しかできません。
2回目以降の回答はお断りします。
また、解答後すぐにはコメントが反映されません。
(反映されると答えが見えてしまうため)
ご了承ください。
解答受付は終了しました
5882353について
5882353は面白い特徴を持った数で、
5882353=5882+23532がなりたつ。
一見しただけでは普通のテキトーな数にしか見えないので、よけいに不思議である。
もちろん、同じような数を見つけたくなる。
\(x^2+y^2=10^nx+y\)(\(x,y,n\)は自然数、\(10^n>y\))について考察する。
まず、平方完成による考察から。
\(x^2+y^2=10^nx+y\)
\(x^2–10^nx+y^2–y=0\)
\((2x^2–10^n)^2+(2y-1)^2=10^2n+1\)
つまり、\(10^2n-1\)を平方数の和にすればいいことになる。
\(n=2\)の場合を例にすると、10001を平方数の和にすればいいので、
10001=1002+12=762+652
あとは簡単で、この場合 1233=122+332 と 8833=882+332 が成り立つ。
しかし、この方法で大きなものを見つけようとすると、
大変大きな数を2つの平方数の和にする必要があるため、実用的ではない。
大きな解を見つける方法はないのか?
ところで、5882353x17=100000001=108+1である。
これはきれいだ。というよりはこれだから5882353=5882+23532がなりたっているのか?
ためしに588と2353をそれぞれ17倍すると、9996と40001になる。
すなわち\(588=\cfrac{10^4-4}{17},2353=\cfrac{4\times10^4+1}{17}\)となる。
何か規則性がプンプンにおうので、下のように一般化してみた。
\(x=\cfrac{10^a-b}{b^2+1},y=\cfrac{10^ab+1}{b^2+1}\)とする。
このとき
\(x^2+y^2=\cfrac{(10^a-b)^2+(10^ab+1)^2}{(b^2+1)^2}\)
\(=\cfrac{(b^2+1)(10^2a+1)}{(b^2+1)^2}\)
\(=\cfrac{10^2a+1}{b^2+1}\)
\(10^ax+y=\cfrac{10^a(10^a-b)+10^ab+1}{b^2+1}\)
\(=\cfrac{10^2a+1}{b^2+1}\)
やはり等しくなった。これは感動ものである。
実は、これで答えがバンバン出せるかというと、そうではない。
\(\cfrac{10^a-b}{b^2+1}\)が整数にならないといけないためである。
(\(\cfrac{10^a-b}{b^2+1}\)が整数になるとき\(\cfrac{10^ab+1}{b^2+1}\)が整数になるのは、案外簡単である)
これはしらみつぶしに頑張るしかない。
たとえば、a=64,b=16という解が見つかるが、この場合
389105058365758754863813229571984435797665369649805447470817122 +
6225680933852140077821011673151750972762645914396887159533073932 =
38910505836575875486381322957198443579766536964980544747081712622568093385214007782101167315175097276264591439688715953307393
というとんでもないくらい大きな解になる。
これも計算が大変そうだ。しかし、これはフェルマーの小定理を使って
格段に解の候補を減らせるので、こちらのほうが楽である。
5882353=5882+23532がなりたつ。
一見しただけでは普通のテキトーな数にしか見えないので、よけいに不思議である。
もちろん、同じような数を見つけたくなる。
\(x^2+y^2=10^nx+y\)(\(x,y,n\)は自然数、\(10^n>y\))について考察する。
まず、平方完成による考察から。
\(x^2+y^2=10^nx+y\)
\(x^2–10^nx+y^2–y=0\)
\((2x^2–10^n)^2+(2y-1)^2=10^2n+1\)
つまり、\(10^2n-1\)を平方数の和にすればいいことになる。
\(n=2\)の場合を例にすると、10001を平方数の和にすればいいので、
10001=1002+12=762+652
あとは簡単で、この場合 1233=122+332 と 8833=882+332 が成り立つ。
しかし、この方法で大きなものを見つけようとすると、
大変大きな数を2つの平方数の和にする必要があるため、実用的ではない。
大きな解を見つける方法はないのか?
ところで、5882353x17=100000001=108+1である。
これはきれいだ。というよりはこれだから5882353=5882+23532がなりたっているのか?
ためしに588と2353をそれぞれ17倍すると、9996と40001になる。
すなわち\(588=\cfrac{10^4-4}{17},2353=\cfrac{4\times10^4+1}{17}\)となる。
何か規則性がプンプンにおうので、下のように一般化してみた。
\(x=\cfrac{10^a-b}{b^2+1},y=\cfrac{10^ab+1}{b^2+1}\)とする。
このとき
\(x^2+y^2=\cfrac{(10^a-b)^2+(10^ab+1)^2}{(b^2+1)^2}\)
\(=\cfrac{(b^2+1)(10^2a+1)}{(b^2+1)^2}\)
\(=\cfrac{10^2a+1}{b^2+1}\)
\(10^ax+y=\cfrac{10^a(10^a-b)+10^ab+1}{b^2+1}\)
\(=\cfrac{10^2a+1}{b^2+1}\)
やはり等しくなった。これは感動ものである。
実は、これで答えがバンバン出せるかというと、そうではない。
\(\cfrac{10^a-b}{b^2+1}\)が整数にならないといけないためである。
(\(\cfrac{10^a-b}{b^2+1}\)が整数になるとき\(\cfrac{10^ab+1}{b^2+1}\)が整数になるのは、案外簡単である)
これはしらみつぶしに頑張るしかない。
たとえば、a=64,b=16という解が見つかるが、この場合
389105058365758754863813229571984435797665369649805447470817122 +
6225680933852140077821011673151750972762645914396887159533073932 =
38910505836575875486381322957198443579766536964980544747081712622568093385214007782101167315175097276264591439688715953307393
というとんでもないくらい大きな解になる。
これも計算が大変そうだ。しかし、これはフェルマーの小定理を使って
格段に解の候補を減らせるので、こちらのほうが楽である。
x^2+y^2=n(z^2)の自然数解(2)
前回分はこちら
x^2+y^2=n(z^2)の自然数解(1)
ここから、\(n\)を一般的にして考えてみる。
途中の式変形から考えると、
\(n\)が2個の平方数の和で表されるとき、\(x^{2}+y^{2}=nz^{2}\)の解は無数に存在するのでは?
検証しよう。
\(n=a^2+b^2\)(\(a,b\)は自然数) と表されるとき、
\(x^{2}+y^{2}=z^{2}\)
\((a^2+b^2)x^{2}+(a^2+b^2)y^{2}=(a^2+b^2)z^{2}\)
\((a^{2}x^{2}+2abxy+b^{2}y^{2})+(b^{2}x^{2}-2abxy+a^{2}y^{2})=(a^2+b^2)z^{2}\)
\((ax+by)^{2}+(bx-ay)^{2}=(a^2+b^2)z^{2}\)
\((ax+by)^{2}+(bx-ay)^{2}=nz^{2}\)
やはりそうだ。
\(n\)が2個の平方数の和で表されるとき、\(x^{2}+y^{2}=nz^{2}\)の解は無数に存在する。
では、その裏は…?
\(n\)が2個の平方数の和で表されないとき、\(x^{2}+y^{2}=nz^{2}\)の解は存在しない
これが解けるのか?これは自分の力ではわからなかった。
ということで、Wikipedia先生に相談してみたら、答えが見つかった。
Wikipedia先生によると、これはオイラーが解決した問題に近く、
解き方はこうである。
出典元:Wikipedia - 二個の平方数の和
これとこの事実を合わせて使う。
1: 4を法として1に合同な素数は二つの平方数の和として表せる。
2: 素因数がすべて4を法として1に合同な素数となる合成数も、
二つの平方数の和として表せる。
そうすると、
(1) \(n\)は4を法として3に合同な素因数を持つ。
(2) しかし\(x^2+y^2\)は4を法として3に合同な素因数を持たないため、
\(x^{2}+y^{2}=nz^{2}\)の解は存在しない。
以上のことが言える。
結構奥が深い問題だったなぁ…。
x^2+y^2=n(z^2)の自然数解(1)
ここから、\(n\)を一般的にして考えてみる。
途中の式変形から考えると、
\(n\)が2個の平方数の和で表されるとき、\(x^{2}+y^{2}=nz^{2}\)の解は無数に存在するのでは?
検証しよう。
\(n=a^2+b^2\)(\(a,b\)は自然数) と表されるとき、
\(x^{2}+y^{2}=z^{2}\)
\((a^2+b^2)x^{2}+(a^2+b^2)y^{2}=(a^2+b^2)z^{2}\)
\((a^{2}x^{2}+2abxy+b^{2}y^{2})+(b^{2}x^{2}-2abxy+a^{2}y^{2})=(a^2+b^2)z^{2}\)
\((ax+by)^{2}+(bx-ay)^{2}=(a^2+b^2)z^{2}\)
\((ax+by)^{2}+(bx-ay)^{2}=nz^{2}\)
やはりそうだ。
\(n\)が2個の平方数の和で表されるとき、\(x^{2}+y^{2}=nz^{2}\)の解は無数に存在する。
では、その裏は…?
\(n\)が2個の平方数の和で表されないとき、\(x^{2}+y^{2}=nz^{2}\)の解は存在しない
これが解けるのか?これは自分の力ではわからなかった。
ということで、Wikipedia先生に相談してみたら、答えが見つかった。
Wikipedia先生によると、これはオイラーが解決した問題に近く、
解き方はこうである。
出典元:Wikipedia - 二個の平方数の和
すばらしい。\(A=x^2+y^2\)が\(p\equiv3\;(\operatorname{mod}\;4)\)の形の素因数を持つと仮定して矛盾を導く(背理法)。\(p|a\)であれば
\(A=pa=x^2+y^2\)
と書ける。ここで\(p|x\)であれば必然的に\(p|y\)であり、\(p^2|A\)であるから両辺を\(p^2\)で除するものとする。\(p\not|x\)であれば\(xx^{-1}\equiv1\;(\operatorname{mod}\;p)\)となる\(x^{-1}\)が存在する。両辺に\((x^{-1})^2\)を乗すると\(pa(x^{-1})^2=1+(yx^{-1})^2\)\(\equiv{1+(yx^{-1})^2}\;(\operatorname{mod}\;p)\)\(\equiv{(yx^{-1})^2}\;(\operatorname{mod}\;p)\)
となる。しかし、これは\(-1\)が\(p\equiv3\;(\operatorname{mod}\;4)\)の平方剰余にならないという事実に反する。従って、\(p\equiv3\;(\operatorname{mod}\;4)\)の形の素因数を平方以外の形で持つ合成数が二個の平方数の和で表されることはない。
これとこの事実を合わせて使う。
1: 4を法として1に合同な素数は二つの平方数の和として表せる。
2: 素因数がすべて4を法として1に合同な素数となる合成数も、
二つの平方数の和として表せる。
そうすると、
(1) \(n\)は4を法として3に合同な素因数を持つ。
(2) しかし\(x^2+y^2\)は4を法として3に合同な素因数を持たないため、
\(x^{2}+y^{2}=nz^{2}\)の解は存在しない。
以上のことが言える。
結構奥が深い問題だったなぁ…。