問題コーナー(第1回)解答
この問題は意外な答えになります。
1:正弦定理による解答
△PBA∽△ABCより
\(\cfrac{BC}{\sin(\angle BAC)}=\cfrac{BA}{\sin(\angle BCA)}\)
\(\sin(\angle BAC)=\cfrac{1+\sqrt{5}}{4}\)
2:初等幾何による解答
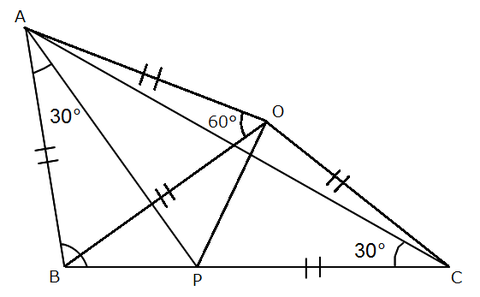
問題
三角形ABCがある。辺BC上にAB=PCとなる点Pを取ったところ、角PAB=角ACBとなった。
このとき、角ABCを求めよ。ただし角ABCは鈍角(90度より大きい)とする。
1:正弦定理による解答
△PBA∽△ABCより
BP:BA=BA:(BP+PC),BP(BP+PC)=BA^2
またBA=PCより、BC=\(\cfrac{1+\sqrt{5}}{2}BA\)
これを使うと、正弦定理より
\(\cfrac{BC}{\sin(\angle BAC)}=\cfrac{BA}{\sin(\angle BCA)}\)
\(\cfrac{\frac{1+\sqrt{5}}{2}BA}{\sin(\angle BAC)}=\cfrac{BA}{\frac{1}{2}}\)
\(\sin(\angle BAC)=\cfrac{1+\sqrt{5}}{4}\)
ここから、何とかして∠BAC=54°と求め、∠ABC=96°と求める。
2:初等幾何による解答

△ABCの外心をOとすると、
AO=BO=CO、また∠AOB=2∠ACB=60°
よって△AOBは正三角形で、AB=PC=AO=BO=CO
そして、△ABPと△AOPにおいて
共通よりAP=AP…①、△AOBは正三角形よりAB=AO…②
また∠BAP=30°、∠OAP=∠OAB-∠BAP=30°より
∠BAP=∠OAP…③
①,②,③より△ABP≡△AOP、BP=OP
ここで∠OBP=θとおくと
∠BOP=θ,∠OPC=2θ,∠POC=2θ,∠OCP=θより
5θ=180°,θ=36°