準備
円の「反転」という操作を使います。
これについてはここでは詳しく述べませんが、このサイトにある程度かかれています。
mathtrain.jp
ここで使う反転の性質は
「反転の中心を通らない円を反転させると円になる」
というものです。
これから、
「点\(A,B,C,D\)を反転させた点\(A',B',C',D'\)が同一円周上にあり、その円が反転の中心を通らないことと、点\(A,B,C,D\)が同一円周上にあり、その円が反転の中心を通らないことは同値である。」 …事実1
ということもわかります。
また、次の性質も成り立ちます。
「点\(P\)から円\(\Gamma\)に接線が引かれていて、それぞれの円との接点をそれぞれ\(A,B\)とする。点\(A,B\)の中点を点\(M\)とするとき、点\(P\)を反転させると点\(M\)に移る。」 …事実2

証明
円\(\Gamma\)の中心を\(O\)とする。点\(O,M,P\)が一直線上にあることは明らか。このとき、\(\angle OAP=\angle OMA=90^\circ\)より\(\triangle OAP \sim \triangle OMA\)。よって\(OM:OA=OA:OP\)より\(OP\cdot OM=OA^2\)となり結果が従う。
そして、次ですが、反転とは関係がありませんが四角形についてこの性質が成り立ちます(よく知られた事実です)。
「四角形のそれぞれの辺の中点を結ぶと平行四辺形ができる。」 …事実3

証明は略しますが、中点連結定理で簡単に証明できます。(図参照)
では、円に内接もするし外接もする四角形について考えていきましょう。
四角形\(ABCD\)が円\(\Gamma\)に外接していると仮定します。
そして辺\(AB,BC,CD,DA\)と円\(\Gamma\)の接点をそれぞれ\(P,Q,R,S\)とします。

すると四角形\(PQRS\)ができますね。
辺 の中点をそれぞれ\(A',B',C',D'\)とします。すると、点\(A',B',C',D'\)は点\(A,B,C,D\)を反転させた点となります。これは事実2からわかります。
の中点をそれぞれ\(A',B',C',D'\)とします。すると、点\(A',B',C',D'\)は点\(A,B,C,D\)を反転させた点となります。これは事実2からわかります。

ここでは円に内接もするし外接もする四角形について考えているので、\(A,B,C,D\)が同一円周上にあるときについて考えます。
ここで事実1を用いましょう。点\(A',B',C',D'\)が同一円周上にある条件がわかれば、いつ\(A,B,C,D\)が同一円周上にあるかがわかります。(注)
そして事実3。点\(A',B',C',D'\)は四角形\(PQRS\)の辺のそれぞれの中点を結んでできた四角形だったので、四角形\(A'B'C'D'\)は平行四辺形だとわかります。

では、「円に内接する平行四辺形」とはなんでしょうか?対角の和が180°でなくてはいけないため、そのような平行四辺形は長方形だとわかります。すなわち、四角形\(A'B'C'D'\)は長方形だとわかります。
というわけで、
「四角形\(ABCD\)が円に内接もするし外接もする←→四角形\(A'B'C'D'\)が長方形」
ということがわかりました。

しかし「四角形\(A'B'C'D'\)が長方形」という条件がわかりにくいですね…しかし、\(PR\perp QS\)という条件と同値なのは中点連結定理によってわかります。
というわけで、いろいろ長くなりましたが、最終的には
「四角形\(ABCD\)が円に内接もするし外接もする←→\(PR\perp QS\)」
ということがわかります。

けっこう簡単な条件で表せました。
これをつかうと簡単に円に内接もするし外接もする四角形をかけて楽しいですよ!
注:四角形\(A'B'C'D'\)の外接円が反転の中心を通らないということを厳密に証明できていません。証明しようとなると大変そう…

とおきます。

の延長に
となるように点
を、
の延長に
となるように点
をとります。

が平行四辺形となるように、
となるように点
をとります。

に関して点
と同じ側に、
が正三角形となるように点
をとります。

より
となります。
、
より点
は三角形
の外心となるので、
となります。よって
です。
がわかり、
がわかります。
となります。
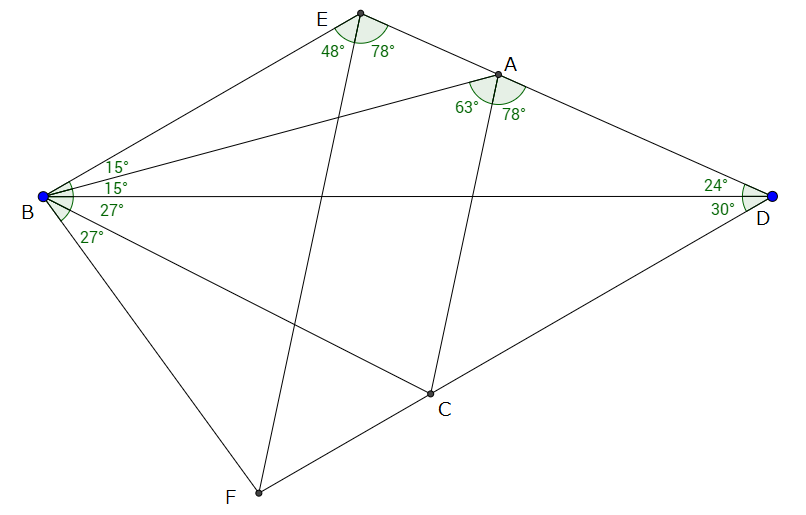
は平行四辺形なので、
より、
です。
より
なので
となります。
より
。よって
です。
より
。
となり、これが答えです。









