昔、こんな感じで線を引いて遊んだことがあるのだが…。
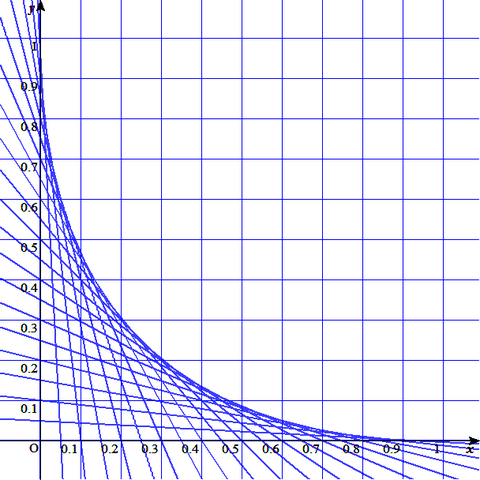
0と1、0.1と0.9、0.2と0.8、…と線を結んでいくと、なんだか曲線が見えてくる。
直線が曲線を作るのは、かなり不思議である。
で、中1の時にこんなことが疑問に思った。
「この曲線はどのような式であらわされるのだろう?」
当時、微分っぽいことをするのはわかったが、具体的な求め方はわからなかった。
それから6か月後解けたので、その方法を紹介する。
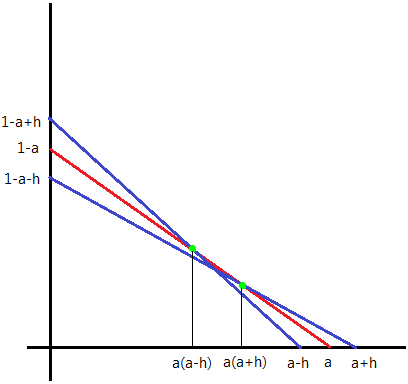
あの曲線とそれを作っている任意の直線は接すると考えていい。
まず0<a<1を満たす実数aについて、
直線 \(y=-\frac{1-a}{a}x+1-a\) と \(y=-\frac{1-a-h}{a+h}x+1-a-h\) の交点を計算すると、
計算はめんどくさいが、x座標がa(a+h)のとき2直線が交わることがわかる。
同じように、直線 \(y=-\frac{1-a}{a}x+1-a\) と \(y=-\frac{1-a+h}{a-h}x+1-a+h\) の交点を計算することで
x座標がa(a-h)のとき2直線が交わることがわかる。
このhをだんだんと小さくすることで、この2つの交点はそれぞれ
だんだんとx座標が\(a^2\)に近くなっていく。
この近づいた点があの曲線との接線となるので、
任意の直線\(y=-\frac{1-a}{a}x+1-a\)とあの曲線は
x座標が\(a^2\)の点で接すると考えていい。
\(y=-\frac{1-a}{a}x+1-a\)に\(x=a^2\)を代入することで、
点\((a^2,(1-a)^2)\)があの曲線を通るということがわかる。
\(x=a^2,y=(1-a)^2\)でaが0~1の値を動くときのグラフは、
\(\sqrt{x}+\sqrt{y}=1\)のグラフに等しい。
よってこの曲線は\(\sqrt{x}+\sqrt{y}=1\)である。
ちなみにこれは放物線である。(行列変換で\(\frac{\pi}{4}\)回転させるとわかる。)
この曲線が放物線になるのは意外だった。
Wikipediaによると、これは「包絡線」というらしい。
包絡線 - Wikipedia